guia-tp

Práctica 5: Árboles

En cada caso se debe implementar el TAD descripto y una aplicación que, utilizando el tipo abstracto de dato, permita al usuario el ingreso de una o más instancias (según sea necesario), la aplicación de cualquiera de las operaciones y luego la obtención del resultado.

Para empezar a trabajar

Construir el TAD de Arboles correspondiente a la implementación de “Punteros” teniendo en cuenta:

• Definir las estructuras de datos en función a las especificaciones dadas en clase y documentadas en los PDF que se encuentran en el aula virtual de la asignatura.
• Se las debe implementar respetando estrictamente los nombres y parámetros de cada una de las operaciones del TAD especificadas.
• Se lo debe probar y testear de forma tal que se pueda asegurar que el TAD funciona correctamente.

Arboles Binarios

Analizando los árboles binarios

Dado un árbol binario no vacío, se pide implementar funciones que retornen:

• Una lista con los nodos terminales u hojas.
• Una lista con todos los nodos interiores (los que no son ni hojas ni raíz)
• Un booleano que determine si todas las hojas están en el mismo nivel.
• Una lista con todas las posiciones de las ocurrencias de una clave dentro del arbol.

Determinar la complejidad algorítmica de las soluciónes.

Conociendo los nodos

Para un nodo del árbol binario determinado, se pide implementar funciones que retornen:

• El nombre del nodo padre.
• Una lista con todos sus hijos.
• Una lista con su nodo hermano.
• El nivel en el que se encuentra.
• La altura de su rama (Altura del Subárbol).
• Una lista con todos los nodos que están en el mismo nivel.
• Un booleano que determine si es equivalente con otro arbol binario dado.

Arboles N-arios

Analizando los árboles

Un árbol n-ario puede ser representado como binario utilizando la transformación de Knuth. Esto puede ser útil para manejar árboles n-arios en estructuras de almacenamiento fijo, sin necesidad de conocer el “n” del árbol.

Se propone un árbol binario derivado del n-ario, tal que para cada nodo del árbol n-ario, su primer hijo es el hijo izquierdo en el árbol binario, y los hermanos de cada nodo son sus hijos derechos.

Ejemplo: (n-ario a la izquierda, representado en binario a la derecha)

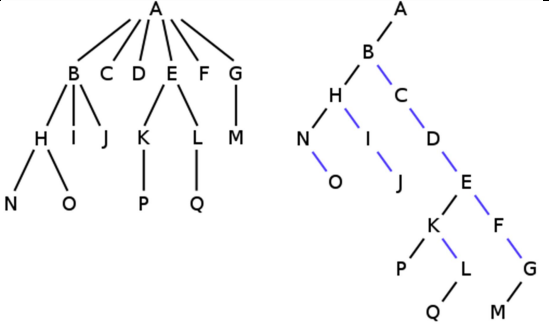
Dado un árbol N-ario, se pide implementar funciones que retornen:

• La altura del mismo.
• El nivel de un nodo.
• Una lista con todos las claves de los nodos internos.
• Un booleano que determine si todas las hojas están al mismo nivel.
• Una lista con el resultado del recorrido en anchura del árbol.
• La cantidad de hojas de dicho árbol.
• Un booleano, que dados dos árboles generales, determine si tienen la misma estructura, sin importar los datos del mismo (árbol similar).
• El padre de un nodo del árbol.
• Una lista con los hermanos de un nodo del árbol.

Arboles Binarios de Búsqueda Balanceados (AVL)

Insertar y Eliminar

• Mostrar el resultado de insertar 5, 3, 8, 15, 9, 13, 6, 11, 10 y 12 en un árbol. AVL inicialmente vacío (indicando las rotaciones realizadas).
• Dibujar el árbol AVL que resulta de realizar las siguientes inserciones: 7, 11, 10, 2, 22, 8, 4, 21, 13. A continuación, eliminar los elementos: 8, 4, 7.
• Realizar las operaciones que se detallan, marcando para cada nodo su factor de equilibrio en cada momento. En caso de producirse desequilibrio, indicar la causa y explicar con detalle qué operación se ha utilizado para resolverlo.
  • Inserciones: 15, 11, 12, 9, 19, 10, 14, 16 y 25.
  • Eliminaciones: 14, 15 y 10.

Árboles B y B+

¿Cómo funcionan?

• Dibujar el árbol B de orden 5, resultado de insertar los siguientes datos: 3, 6, 13, 2, 5, 8, 4, 19, 15, 9, 21, 11.
• Dibujar el árbol B de orden 5 que resulta a partir de la siguiente entrada de datos: A, D, M, P, Z, B, J, N, G, U, R, K, E, H, O, L, F, S, C, T.
• Dibujar el árbol B de orden 5 que resulta de realizar las siguientes inserciones: 11, 7, 6, 2, 1, 14, 18, 13, 10, 5, 21, 19, 16, 24, 31, 12, 4, 22 y 28.
• A continuación, eliminar los elementos: 18, 11 y 16.

Ejercicios de Implementación

Arbol de Expresión

Escribir un algoritmo que determine si un árbol binario cargado puede ser un árbol de expresión.

Ver en la bibliografía o PDF de la asignatura qué es un árbol de expresión. También pueden consultarse más detalles en el siguiente enlace.

Características de un árbol de expresión:

• La raíz siempre debe ser un operador.
• La raíz de todo subárbol siempre es un operador.
• Las hojas siempre deben ser operandos.
• Los nodos internos deben estar etiquetados por operadores.
• Si un operador tiene mayor prioridad que el que está almacenado en un nodo, se coloca como hijo del mismo.
• Si un operador tiene igual o menor prioridad que el que está en un nodo, se coloca como padre de éste.
• Una expresión entre paréntesis tiene mayor prioridad que cualquier otra.
• Un nodo puede contener como hijo un subárbol que contiene una pequeña expresión.- Los paréntesis no se representan porque no son necesarios.

Comparando árboles

Binario vs. AVL

Generar un algoritmo, recursivo o no, que permita construir un árbol binario de búsqueda balanceado (AVL) a partir de un árbol binario sin un orden determinado.

Comparar las alturas de ambos árboles.

Determinar la complejidad algorítmica.

Binario de Búsqueda vs. AVL

Cargar la misma serie de números en un árbol binario de búsqueda y en un árbol binario balanceado “AVL”.

Comparar la altura de ambos árboles. Repetir el proceso n veces. ¿Qué puede concluir al respecto?

AVL vs. B vs. B+

Dada una serie de números generados al azar, cargarla en un árbol binario de búsqueda balanceado (AVL), en un Árbol “B” y “B+”. Comparar la altura de los árboles.

Repetir el proceso n veces. Se debe poder ingresar la cantidad de claves a generar al azar, la cantidad de repeticiones n que se desea ejecutar el proceso.

¿Qué puede concluir al respecto?

Texto predictivo (LITE)

Se necesita armar un proceso que pueda ir almacenando palabras a medida que se van “tipeando”, cuando uno va escribiendo que trate de inferir de que palabra se trata.

Usar un árbol para resolver el problema (similar a los diccionarios de los celulares por ejemplo).

Se pide:

• Tener una opción para ver el diccionario que tiene.
• Retornar en orden descendente de la palabra más usada a la menos usada, con la cantidad de apariciones.
• Permitir escribir usando el diccionario, donde nos vaya dando las 5 palabras que podrían coincidir con lo que vamos escribiendo.

This site is open source. Improve this page.